AVL tree

AVL tree is a balanced binary search tree with a height \(O(\log n)\) when there are \(n\) nodes. This ensures that operations on a set implemented using an AVL tree have time complexity \(O(\log n)\).

Balance condition

An AVL tree maintains the following balance condition: For each node, the heights of the left subtree and the right subtree cannot differ by more than \(1\).

In the following image, the tree on the left satisfies the balance condition, but the tree on the right does not, because the heights of the subtrees of the node \(3\) are \(0\) and \(2\).

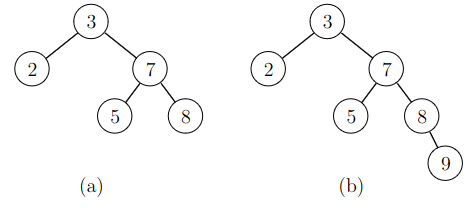
The balance condition means that the nodes are relatively evenly distributed to different areas of the tree, which ensures that the height is \(O(\log n)\). This can be proven by calculating how the height depends on the number of nodes.

Let \(f(h)\) be the smallest number of nodes possible for an AVL tree of height \(h\). The first values of the function are \(f(0)=1\) and \(f(1)=2\). For larger heights, the function can be computed using the formula

because the smallest tree of height \(h\) is obtained by having the smallest tree of height \(h-2\) as one subtree and the smallest tree of height \(h-1\) as the other subtree. For example, \(f(2)=f(0)+f(1)+1=4\) and \(f(3)=f(1)+f(2)+1=7\).

With this we can find an estimate on the maximum height of a tree with \(n\) nodes. The maximum height is the largest \(h\) such that \(f(h) \le n\), because any tree of height more than \(h\) would need to have more than \(n\) nodes.

When \(h \ge 2\), we can estimate the value \(f(h)\) as follows:

Based on this, \(f(h) > 2^{h/2}\), which means that \(h\) cannot be bigger than \(2 \log_2(n)\) if \(f(h) \le n\). Thus the height of an AVL tree is \(O(\log n)\).

Heights and rotations

An AVL tree can be implemented similarly to an ordinary binary search tree. The difference is that after adding or removing an element, we must make sure that the balance condition is still satisfied.

Since the balance condition depends on the heights of subtrees, it is useful for each node to store the height of its subtree. This way the subtree heights are easily obtained whenever needed.

If the balance condition is violated, the situation can be corrected using rotations in the tree. The following image illustrates the rotations in an AVL tree:

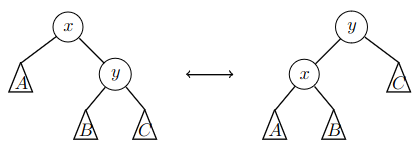
Here \(x\) and \(y\) are nodes of the tree and \(A\), \(B\) and \(C\) are subtrees. A rotation in one direction raises \(y\) up and pushes \(x\) down, and a rotation in the other direction does the opposite. These rotations can be used for changing the heights of subtrees without violating the ordering condition of binary search trees.

Adding an element

When an element is added to the tree, the subtree heights may change for the nodes on the route from the new node to the root. After the addition, these nodes are visited starting from the bottom and the heights are updated if necessary. If the update of a height causes a violation of the balance condition, the situation is corrected with rotations.

Let \(x\) denote the lowest node that violates the balance condition. Let \(y\) denote the child of \(x\) on the route from the new node and let \(z\) denote the child of \(y\) on the same route. We will consider two possible cases:

Case 1

The nodes \(y\) and \(z\) are children of the same side. In this case, we do a rotation that raises \(y\) up and pushes \(x\) down.

For example, in the following image, \(y\) and \(z\) are both right children. Then the rotation moves \(x\) to the left child of \(y\) while \(z\) remains the right child of \(y\).

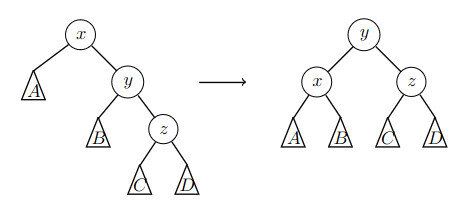
If \(y\) and \(z\) are both left children, a symmetric rotation to the opposite direction is performed.

Consider the following example tree:

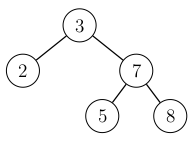
When an element \(9\) is added to the tree, its location in the tree is chosen as in any binary search tree:

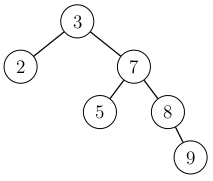
After the addition, we traverse upwards from the new node towards the root. The balance condition is violated for the root (but not for the other nodes on the route), because the height of the left subtree is \(0\) but the new height of the right subtree is \(2\). This corresponds to the above situation, where \(x=3\), \(y=7\) and \(z=8\).

The violation is corrected with a rotation that moves the node \(7\) up and the node \(3\) down:

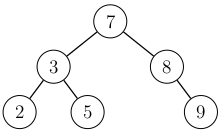
After the rotation, the tree is balanced.

Case 2

The nodes \(y\) and \(z\) are children of different sides. Then we need two rotations: first the node \(z\) is raised up and \(y\) is pushed down, and then the node \(z\) is raised up again and the node \(x\) is pushed down.

For example, in the following image, the node \(y\) is a right child and the node \(z\) is a left child. After the rotations, \(x\) is the left child and \(y\) the right child of \(z\).

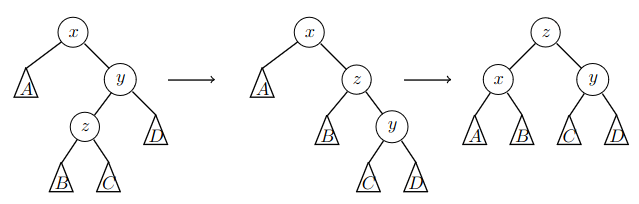
If \(y\) is a left child and \(z\) is a right child, symmetric rotations in the opposite direction are performed.

Consider the following example tree:

When an element \(6\) is added, its location in the tree is chosen as in any binary search tree:

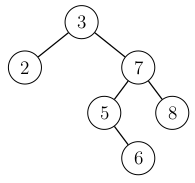
After the addition, the route from the new node to the root is traversed. The balance condition is violated in the root, because the height of the left subtree is \(0\) but the new height of the right subtree is \(2\). This corresponds to the above situation, where \(x=3\), \(y=7\) and \(z=5\).

To correct the violation, we first do a rotation that moves the node \(5\) up and the node \(7\) down:

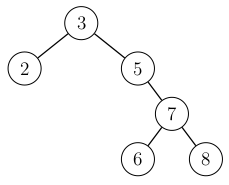
Then another rotation moves the node \(5\) up and the node \(3\) down:

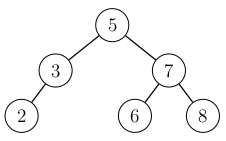
After the rotations, the tree is balanced.

Time complexity

After adding a new node, we traverse to the root and perform rotations if necessary. Since the height of the tree is \(O(\log n)\) and each rotation takes \(O(1)\) time, the total time complexity of addition incuding rotations is \(O(\log n)\). In fact, it can be shown that performing rotations in more than one place per addition is never needed.

Removing an element

Removing an element in an AVL tree can be performed similarly in \(O(\log n)\) time by doing first a standard binary tree removal, and then updating subtree heights on the route to the root and performing rotations to maintain the balance condition when necessary. However, we do not cover element removal in further detail on this course.