Insertion sort

Insertion sort is a simple sorting algorithm with time complexity \(O(n^2)\).

The algorithm goes through the list from left to right. At each position, the element at that position is moved to the left so that the beginning of the list up to that position is in the correct order. When the algorithm has processed all positions, the whole list is in order.

Example

The following picture illustrates the operation of insertion sort when sorting the list \([5,2,4,2,6,1]\).

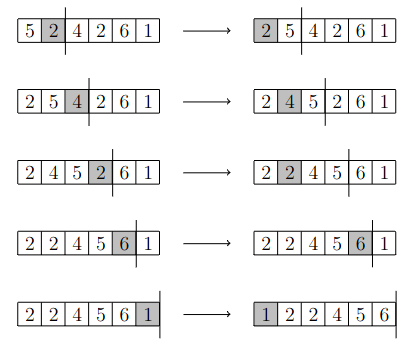
Implementation

Insertion sort can be implemented in Python as follows:

def swap(items, a, b):
    temp = items[a]
    items[a] = items[b]
    items[b] = temp

def insertion_sort(items):
    for i in range(1, len(items)):
        for j in range(i - 1, -1, -1):
            if items[j] > items[j + 1]:
                swap(items, j, j + 1)
            else:
                break
        
numbers = [5, 2, 4, 2, 6, 1]
insertion_sort(numbers)
print(numbers) # [1, 2, 2, 4, 5, 6]

The function insertion_sort sorts the given list using insertion sort. The function has two nested loops. The first loop goes through the list positions from left to right, and the second loop moves the element in the current position to its correct sorted position among the elements up to that position. The moving of elements is done using the function swap that swaps the positions of two elements.

Notice that the above function insertion_sort is intended for illustrating insertion sort and not as an example of the best way to implement sorting in Python. It is better to use the built-in implementations sort and sorted in Python.

Efficiency

The time complexity of insertion sort is \(O(n^2)\) because it has two nested loops. The worst case for the algorithm is if the initial list is in reverse order. Then every element has to be moved all the way to the beginning of the list step by step.

A more precise measure of the efficiency of insertion sort is the number of inversions. A pair of numbers \((a,b)\) is an inversion if \(a<b\) and the list elements at the positions \(a\) and \(b\) are in the wrong order. For example, in the list \([5,2,4,2,6,1]\) the inversions are \((0,1)\), \((0,2)\), \((0,3)\), \((0,5)\), \((1,5)\), \((2,3)\), \((2,5)\), \((3,5)\) and \((4,5)\).

Every swap made by the algorithm removes one inversion from the list, and the final sorted list has no inversions. Thus the number of swaps performed by the algorithm is equal to the number of inversions on the original list. When the list is in reverse order, the number of inversions is \(n(n-1)/2\) which is of order \(O(n^2)\).

Any sorting algorithm that operates by swapping adjacents elements cannot have a better time complexity than \(O(n^2)\). This is because the number of inversion can be \(O(n^2)\) and each swap removes only one inversion. Efficient sorting algorithms move elements more efficiently than by swapping adjacent elements.