Keko
Keko (heap) on tietorakenne, jonka tyypillisiä operaatioita ovat (1) uuden alkion lisääminen, (2) pienimmän/suurimman alkion hakeminen sekä (3) pienimmän/suurimman alkion poistaminen.
Jos keko on minimikeko (min heap), operaatiot (2) ja (3) hakevat ja poistavat pienimmän alkion. Jos taas keko on maksimikeko (max heap), operaatiot (2) ja (3) hakevat ja poistavat suurimman alkion.
Tavallinen keon toteutus on binäärikeko (binary heap), jonka taustalla on puurakenne binääripuu (binary tree). Jokaisella binääripuun solmulla voi olla vasen ja oikea lapsi. Keko on täytetty niin, että alkiot ovat mahdollisimman ylhäällä puussa ja viimeisellä tasolla mahdollisimman vasemmalla.
Minimikeossa jokaisen solmun alkio on yhtä suuri tai suurempi kuin solmun vanhemman alkio. Maksimikeossa puolestaan jokaisen solmun alkio on yhtä suuri tai pienempi kuin solmun vanhemman alkio. Tämän ansiosta minimikeon juurena on pienin alkio ja maksimikeon juurena on suurin alkio.
Esimerkki
Seuraava minimikeko sisältää alkiot \([1,3,4,5,5,5,7,8,8,9]\):
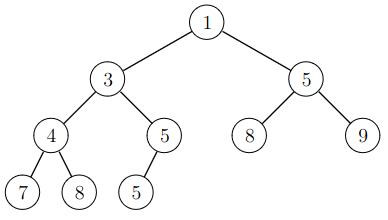
Keon sisältö voidaan esittää listana, joka sisältää keon alkiot taso kerrallaan ylhäältä alas. Esimerkiksi yllä olevaa kekoa vastaa lista \([1,3,5,4,5,8,9,7,8,5]\). Kun alkio on listassa kohdassa \(k\), sen vasen lapsi on kohdassa \(2k+1\), oikea lapsi on kohdassa \(2k+2\) ja vanhempi on kohdassa \(\lfloor (k-1)/2 \rfloor\). Esimerkiksi alkio \(3\) on kohdassa \(1\), sen lapset ovat kohdissa \(3\) ja \(4\) ja sen vanhempi on kohdassa \(0\).
Alkion lisääminen kekoon
Uusi alkio lisätään uudeksi solmuksi keon pohjalle listan loppuun. Tämän jälkeen alkiota nostetaan ylöspäin taso kerrallaan, kunnes se on oikealla paikalla keossa. Joka vaiheessa vaihdetaan keskenään solmun ja sen vanhemman sisältö.
Seuraava kuva näyttää, miten alkio \(2\) voidaan lisätä kekoon. Alkio lisätään aluksi keon pohjalle, minkä jälkeen se nostetaan kaksi tasoa ylöspäin.
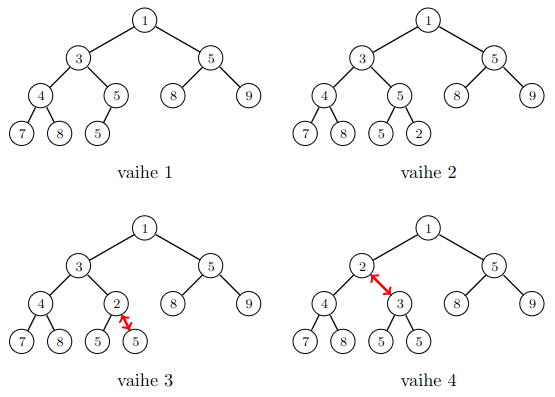
Alkion lisääminen vie aikaa \(O(\log n)\), koska alkio nousee jonkin määrän tasoja ylöspäin keossa ja keon tasojen määrä on \(O(\log n)\).
Alkion poistaminen keosta
Keon juuressa oleva alkio voidaan poistaa siirtämällä sen tilalle keon viimeinen alkio. Tämän jälkeen juuressa olevaa alkiota lasketaan alaspäin taso kerrallaan, kunnes se on oikealla paikalla keossa.
Seuraava kuva näyttää, miten pienin alkio \(1\) voidaan poistaa keosta. Sen tilalle siirretään keon pohjalta alkio \(5\), joka lasketaan sitten alaspäin.
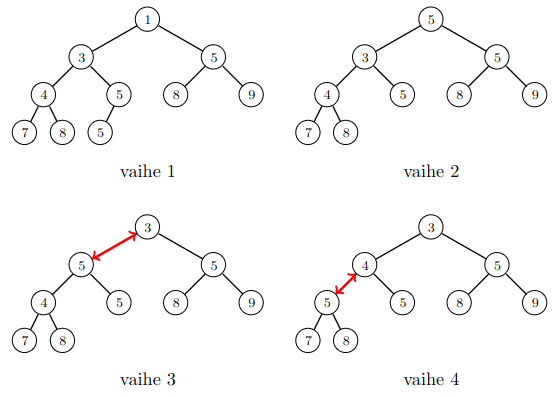
Alkion lisääminen vie aikaa \(O(\log n)\), koska alkio laskeutuu jonkin määrän tasoja alaspäin keossa ja keon tasojen määrä on \(O(\log n)\).
Keon käsittely listana
Pythonin keon toimintaa on helppoa tutkia, koska keon sisältö on aina saatavilla listana. Esimerkiksi seuraava koodi näyttää, miten lista muuttuu, kun lisätään ja poistetaan alkio äskeisten esimerkkien mukaisesti.
import heapq
heap = [1, 3, 5, 4, 5, 8, 9, 7, 8, 5]
heapq.heappush(heap, 2)
print(heap) # [1, 2, 5, 4, 3, 8, 9, 7, 8, 5, 5]
heap = [1, 3, 5, 4, 5, 8, 9, 7, 8, 5]
heapq.heappop(heap)
print(heap) # [3, 4, 5, 5, 5, 8, 9, 7, 8]
Moduulissa heapq on saatavilla myös funktio heapify, joka muuttaa olemassa olevan listan keoksi:
import heapq
items = [8, 7, 6, 5, 4, 3, 2, 1]
heapq.heapify(items)
print(items) # [1, 4, 2, 5, 8, 3, 6, 7]
Funktion heapify aikavaativuus on \(O(n)\), eli sen käyttäminen on tehokkaampaa kuin suorittaa \(n\) kertaa funktio heappush tyhjään kekoon. Tässä kuluisi aikaa \(O(n \log n)\), koska funktio heappush vie aikaa \(O(\log n)\).