Lisäysjärjestäminen

Lisäysjärjestäminen (insertion sort) on yksinkertainen järjestämisalgoritmi, jonka aikavaativuus on \(O(n^2)\).

Algoritmi käy läpi listan kohdat vasemmalta oikealle. Jokaisessa listan kohdassa algoritmi siirtää kyseisessä kohdassa olevaa alkiota sopivan määrän vasemmalle niin, että listan alkuosa kyseiseen kohtaan asti on järjestyksessä. Kun algoritmi on käynyt läpi kaikki listan kohdat, koko lista on järjestyksessä.

Esimerkki

Seuraava kuva näyttää, miten lisäysjärjestäminen järjestää listan \([5,2,4,2,6,1]\).

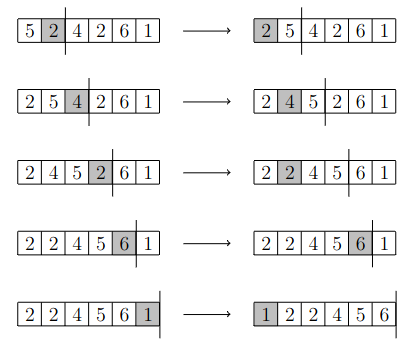
Toteutus

Lisäysjärjestäminen voidaan toteuttaa seuraavasti Pythonilla:

def swap(items, a, b):
    temp = items[a]
    items[a] = items[b]
    items[b] = temp

def insertion_sort(items):
    for i in range(1, len(items)):
        for j in range(i - 1, -1, -1):
            if items[j] > items[j + 1]:
                swap(items, j, j + 1)
            else:
                break
        
numbers = [5, 2, 4, 2, 6, 1]
insertion_sort(numbers)
print(numbers) # [1, 2, 2, 4, 5, 6]

Funktio insertion_sort järjestää sille annetun listan lisäysjärjestämisen avulla. Funktiossa on kaksi sisäkkäistä silmukkaa, joista ensimmäinen käy läpi listan kohdat vasemmalta oikealle ja toinen siirtää käsiteltävän alkion oikealle paikalle listan alkuosassa. Käytössä on apufunktio swap, joka vaihtaa keskenään kaksi listassa olevaa alkiota niiden kohtien perusteella.

Huomaa, että funktion insertion_sort tarkoituksena on havainnollistaa, miten lisäysjärjestäminen toimii, eikä antaa esimerkkiä siitä, miten järjestäminen kannattaa toteuttaa Python-ohjelmoinnissa. Funktion insertion_sort sijasta järjestämiseen kannattaa käyttää Pythonin valmiita menetelmiä (sort tai sorted).

Tehokkuus

Lisäysjärjestäminen vie aikaa \(O(n^2)\), koska se muodostuu kahdesta sisäkkäisestä silmukasta. Pahin tapaus algoritmille on käänteisessä järjestyksessä oleva lista, jossa jokainen alkio täytyy siirtää listan alkuun askel kerrallaan.

Lisäysjärjestämisen tehokkuutta kuvaa tarkemmin listan inversioiden määrä. Lukupari \((a,b)\) on inversio, jos \(a<b\) ja listan alkiot kohdissa \(a\) ja \(b\) ovat väärässä järjestyksessä. Esimerkiksi listassa \([5,2,4,2,6,1]\) inversiot ovat \((0,1)\), \((0,2)\), \((0,3)\), \((0,5)\), \((1,5)\), \((2,3)\), \((2,5)\), \((3,5)\) ja \((4,5)\).

Jokainen lisäysjärjestämisen tekemä kahden alkion vaihto (koodissa funktion swap kutsuminen) poistaa listasta yhden inversion. Niinpä lisäysjärjestämisen vaihtojen määrä on yhtä suuri kuin listan inversioiden määrä. Kun lista on käänteisessä järjestyksessä, inversioiden määrä on \(n(n-1)/2\) eli luokkaa \(n^2\).

Jos järjestämisalgoritmi vaihtaa aina kahden vierekkäin olevan alkion järjestyksen, algoritmin aikavaativuus ei voi olla parempi kuin \(O(n^2)\). Syynä tähän on, että inversioiden määrä voi olla luokkaa \(n^2\) ja jokainen vaihto poistaa vain yhden inversion. Tehokkaat järjestämisalgoritmit pystyvät siirtämään alkioita tehokkaammin kuin vaihtamalla keskenään vierekkäisiä alkioita.