Lomitusjärjestäminen
Lomistusjärjestäminen (merge sort) on tehokas järjestämisalgoritmi, jonka aikavaativuus on \(O(n \log n)\).
Algoritmi järjestää listan rekursiivisesti niin, että se järjestää ensin erikseen listan vasemman ja oikean puoliskon. Tämän jälkeen se yhdistää järjestetyn vasemman ja oikean puoliskon kokonaiseksi järjestetyksi listaksi. Koska vasen ja oikea puolisko ovat valmiiksi järjestyksessä, niiden yhdistäminen voidaan toteuttaa tehokkaasti.
Algoritmi hyödyntää rekursiota niin, että se järjestää listan vasemman ja oikean puoliskon kutsumalla itseään. Rekursio päättyy, kun listalla on vain yksi alkio, jolloin listaa ei tarvitse järjestää vaan se on valmiiksi järjestyksessä.
Esimerkki
Seuraava kuva näyttää, miten lisäysjärjestäminen järjestää listan \([5,1,2,9,7,5,4,2]\).
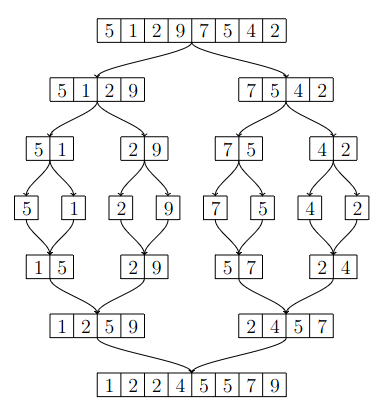
Toteutus
Lomitusjärjestäminen voidaan toteuttaa seuraavasti Pythonilla:
def merge_sort(items):
n = len(items)
if n == 1: return
left = items[0:n//2]
right = items[n//2:]
merge_sort(left)
merge_sort(right)
a = b = 0
for i in range(n):
if b == len(right) or \
(a < len(left) and left[a] < right[b]):
items[i] = left[a]
a += 1
else:
items[i] = right[b]
b += 1
numbers = [5, 2, 4, 2, 6, 1]
merge_sort(numbers)
print(numbers) # [1, 2, 2, 4, 5, 6]
Funktio merge_sort järjestää sille annetun listan lomitusjärjestämisen avulla. Jos listalla on vain yksi alkio, funktio ei tee mitään. Muuten funktio jakaa listan kahteen puoliskoon (left ja right) ja järjestää ne rekursiivisesti.
Puoliskojen järjestämisen jälkeen funktio rakentaa kokonaisen järjestetyn listan. Tämä on toteutettu niin, että funktio käy listan kohdat läpi vasemmalta oikealle ja valitsee jokaiseen kohtaan mahdollisimman pienen jäljellä olevan alkion listasta left tai right. Koska puoliskot ovat järjestyksessä, kummankin puoliskon pienin alkio löytyy tehokkaasti joka vaiheessa.
Huomaa, että funktion merge_sort tarkoituksena on havainnollistaa, miten lomitusjärjestäminen toimii, eikä antaa esimerkkiä siitä, miten järjestäminen kannattaa toteuttaa Python-ohjelmoinnissa. Funktion merge_sort sijasta järjestämiseen kannattaa käyttää Pythonin valmiita menetelmiä (sort tai sorted).
Tehokkuus
Lisäysjärjestämisen aikavaativuus \(O(n \log n)\) johtuu siitä, että algoritmissa on \(O(\log n)\) rekursiivista tasoa ja jokaisella tasolla listojen yhdistäminen vie aikaa \(O(n)\). Rekursiivisten tasojen määrä saadaan siitä, että kun \(n\)-kokoinen lista puolitetaan \(\log n\) kertaa, listalla on vain yksi alkio ja rekursio päättyy.
Tasot muodostuvat seuraavasti:
- Tasolla 1 kaksi \(n/2\)-kokoista listaa yhdistyy yhdeksi \(n\)-kokoiseksi listaksi.
- Tasolla 2 neljä \(n/4\)-kokoista listaa yhdistyy kahdeksi \(n/2\)-kokoiseksi listaksi.
- Tasolla 3 kahdeksan \(n/8\)-kokoista listaa yhdistyy neljäksi \(n/4\)-kokoiseksi listaksi.
- Jne.
Jokaisella tasolla listoissa on yhteensä \(O(n)\) alkiota, minkä takia jokaisen tason listojen yhdistämiset vievät yhteensä aikaa \(O(n)\).