15. Komponentit ja virittävät puut
Tähän mennessä olemme käsitelleet verkkoalgoritmeja, jotka laskevat jotain käymällä läpi verkon kaikki solmut ja kaaret. Tällaiset algoritmit ovat kuitenkin hitaita tilanteessa, jossa verkkoon tulee jatkuvasti muutoksia.
Tässä luvussa tutustumme union-find-rakenteeseen, jonka avulla voidaan pitää tehokkaasti yllä tietoa verkon komponenteista, kun verkkoon lisätään kaaria. Voimme esimerkiksi selvittää tehokkaasti, ovatko solmut samassa komponentissa tai montako komponenttia verkossa on.
Tutustumme myös Kruskalin algoritmiin, joka käyttää union-find-rakennetta verkon pienimmän virittävän puun muodostamiseen. Virittävä puu on verkon kaarten osajoukko, joka yhdistää kaikki verkon solmut toisiinsa.
Union-find-rakenne
Union-find-rakenne on tietorakenne, joka pitää yllä kokoelmaa alkioista. Aluksi jokainen alkio on omassa joukossaan, ja joukkoja voidaan yhdistää. Tietorakenne tarjoaa kaksi tehokasta operaatiota:
- Määritä, mihin joukkoon alkio kuuluu
- Yhdistä kaksi joukkoa samaksi joukoksi
Union-find-rakenne on toteutettu niin, että jokaisessa joukossa yksi alkioista on joukon edustaja. Kaikista muista joukon alkioista on viittaus edustajaan suoraan tai muiden alkioiden kautta. Näiden viittausten avulla voidaan selvittää sen joukon edustaja, johon tietty alkio kuuluu.
Tarkastellaan esimerkkinä union-find-rakennetta, joka sisältää alkiot \(1,2,\dots,8\). Seuraavassa kuvassa joukot ovat \(\{1,4\}\), \(\{2,5,6\}\) sekä \(\{3,7,8\}\):
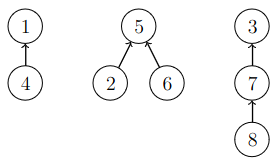
Tässä joukkojen edustajat ovat \(1\), \(5\) ja \(3\). Kaikista muista alkioista päästään viittausten avulla edustajiin. Esimerkiksi alkiosta \(2\) päästään edustajaan polkua \(2 \rightarrow 5\) ja alkiosta \(8\) päästään edustajaan polkua \(8 \rightarrow 7 \rightarrow 3\).
Kaksi alkiota kuuluvat samaan joukkoon, jos niillä on yhteinen edustaja. Esimerkiksi solmut \(2\) ja \(6\) kuuluvat samaan joukkoon, koska molempien joukkojen edustaja on \(5\). Solmut \(2\) ja \(3\) puolestaan kuuluvat eri joukkoihin, koska solmun \(2\) joukon edustaja on \(5\) ja solmun \(3\) joukon edustaja on \(3\).
Kun kaksi joukkoa yhdistetään, toisen joukon edustaja asetetaan viittaamaan toisen joukon edustajaan, josta tulee koko uuden joukon edustaja. Esimerkiksi seuraava kuva näyttää, miten joukot \(\{1,4\}\) ja \(\{2,5,6\}\) voidaan yhdistää:
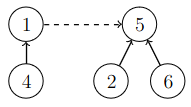
Tässä joukon \(\{1,4\}\) edustaja \(1\) asetetaan viittaamaan joukon \(\{2,5,6\}\) edustajaan \(5\). Tämän seurauksena syntyy uusi joukko \(\{1,2,4,5,6\}\), jonka edustaja on \(5\). Yhdistämisen jälkeen kaikista uuden joukon alkioista pääsee polkua pitkin joukon edustajaan \(5\). Esimerkiksi alkiosta \(4\) päästään edustajaan polkua \(4 \rightarrow 1 \rightarrow 5\).
Union-find-rakenteen tehokkuus riippuu siitä, miten nopeasti tietyn alkion edustaja voidaan löytää. Mitä lyhempiä viittausten muodostamat polut ovat, sitä tehokkaammin edustajat voidaan löytää. Polkujen pituutta voidaan rajata toteuttamalla joukkojen yhdistämiset niin, että ne eivät tuota pitkiä polkuja.
Kun kaksi joukkoa yhdistetään, on kaksi tapaa valita, kumman joukon edustaja alkaa viitata toisen joukon edustajaan. Tehokkuuden kannalta hyvä valinta on, että pienemmän joukon edustaja alkaa viitata suuremman joukon edustajaan. Tällöin jokaisen polun pituus on luokkaa \(O(\log n)\) ja minkä tahansa solmun edustaja voidaan löytää tehokkaasti.
Union-find-rakenne voidaan toteuttaa seuraavasti:
class UnionFind:
def __init__(self, n):
self.link = {node: None for node in range(1, n + 1)}
self.size = {node: 1 for node in range(1, n + 1)}
def find(self, x):
while self.link[x]:
x = self.link[x]
return x
def union(self, a, b):
a = self.find(a)
b = self.find(b)
if a == b: return
if self.size[a] > self.size[b]:
a, b = b, a
self.link[a] = b
self.size[b] += self.size[a]
Sanakirja link ilmoittaa kustakin solmusta, mihin solmuun se viittaa. Jos solmu ei viittaa mihinkään, viittauksen kohdalla on None. Sanakirja size puolestaan kertoo jokaisen joukon edustajasolmulle, kuinka suuri kyseinen joukko on.
Metodi find etsii solmun x edustajan kulkemalla viittausten muodostamaa polkua. Metodi union yhdistää joukot, joihin kuuluvat solmut a ja b. Metodi etsii ensin joukkojen edustajat. Jos solmut ovat jo samassa joukossa, metodi ei tee mitään. Muuten metodi asettaa pienemmän joukon edustajan viittaamaan suuremman joukon edustajaan ja päivittää suuremman joukon edustajaan liittyvän koon.
Seuraava koodi esittelee luokan käyttämistä:
u = UnionFind(8)
u.union(1, 4)
u.union(2, 5)
u.union(5, 6)
u.union(3, 7)
u.union(7, 8)
print(u.find(1)) # 4
print(u.find(2)) # 5
print(u.find(3)) # 7
print(u.find(4)) # 4
print(u.find(5)) # 5
print(u.find(6)) # 5
print(u.find(7)) # 7
print(u.find(8)) # 7
Tässä tapauksessa joukon \(\{1,4\}\) edustaja on \(4\), joukon \(\{2,5,6\}\) edustaja on \(5\) ja joukon \(\{3,7,8\}\) edustaja on \(7\).
Esimerkki: Uudet tiet
Tehtävä
Bittimaassa on \(n\) kaupunkia mutta ei vielä yhtään tietä. Tehtäväsi on laatia luokka NewRoads, jossa on seuraavat metodit:
add_road: lisää tien kahden kaupungin välillehas_route: tarkastaa, pystyykö kahden kaupungin välillä matkustamaan teitä pitkin
Kummankin metodin tulee toimia tehokkaasti.
Tehtävä voidaan ratkaista seuraavasti union-find-rakenteen avulla:
class NewRoads:
def __init__(self, n):
self.uf = UnionFind(n)
def add_road(self, a, b):
self.uf.union(a, b)
def has_route(self, a, b):
return self.uf.find(a) == self.uf.find(b)
Ideana on, että union-find-rakenteen joukot vastaavat verkon komponentteja. Aluksi jokainen alkio on omassa joukossaan, mikä tarkoittaa, että jokainen solmu on omassa komponentissaan.
Metodi add_road kutsuu metodia union, joka yhdistää verkon komponentit. Metodi has_route puolestaan kutsuu kummallekin alkiolle metodia find. Alkiot kuuluvat samaan komponenttiin, jos find antaa niille saman edustajan.
Tässä ratkaisussa kummankin metodin add_road ja has_route aikavaativuus on \(O(\log n)\).
Puut verkoissa
Suuntaamaton verkko on puu (tree), jos verkko on yhtenäinen ja syklitön. Esimerkiksi seuraava verkko on puu:
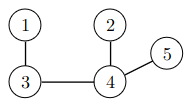
Toisin kuin aiemmin tällä kurssilla käsitellyissä puissa, tässä tapauksessa puussa ei ole juurta eikä solmuilla ole lapsia eikä vanhempia. Kuitenkin puussa on lehtiä: lehtiä ovat kaikki solmut, joiden aste on \(1\) eli joihin liittyy vain yksi kaari. Esimerkiksi yllä olevassa puussa lehtiä ovat solmut \(1\), \(2\) ja \(5\).
Kun verkko on puu ja siinä on \(n\) solmua, siinä on aina tasan \(n-1\) kaarta. Jos puusta poistetaan kaari, se ei ole enää yhtenäinen. Jos taas puuhun lisätään kaari, se ei ole enää syklitön.
Verkon virittävä puu (spanning tree) on puu, joka sisältää verkon solmut ja jonkin osajoukon sen kaarista. Seuraavassa kuvassa on vasemmalla verkko ja oikealla yksi sen virittävistä puista:
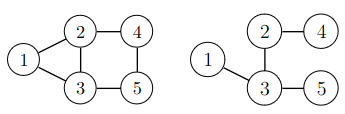
Verkolle voidaan muodostaa yleensä useita erilaisia virittäviä puita, koska on monia tapoja valita kaaria niin, että tuloksena on puu.
Kun verkko on painotettu, virittävän puun paino saadaan laskemalla yhteen puuhun valittujen kaarten painot. Tarkastellaan esimerkkinä seuraavaa kuvaa, jossa on painotettu verkko ja kaksi sen virittävää puuta:

Ensimmäisen virittävän puun paino on \(4+1+2+5=12\), ja toisen virittävän puun paino on \(2+1+2+5=10\).
Tässä tapauksessa toinen virittävä puu on verkon pienin virittävä puu (minimum spanning tree) eli virittävä puu, jonka paino on pienin mahdollinen. Myös pienimmän virittävän puun valintaan voi olla useita mahdollisuuksia.
Kruskalin algoritmi
Kruskalin algoritmi on union-find-rakennetta käyttävä algoritmi, jolla voidaan muodostaa verkon pienin virittävä puu. Algoritmi käy läpi verkon kaaret painojärjestyksessä ja valitsee virittävään puuhun mukaan kaikki kaaret, jotka eivät aiheuta sykliä.
Esimerkiksi äskeisen verkon tapauksessa algoritmi käy läpi kaaret seuraavassa järjestyksessä:
| Kaari | Paino | Mukaan puuhun? |
| \(2-3\) | \(1\) | Kyllä |
| \(1-2\) | \(2\) | Kyllä |
| \(2-4\) | \(2\) | Kyllä |
| \(1-3\) | \(4\) | Ei |
| \(4-5\) | \(5\) | Kyllä |
| \(3-5\) | \(7\) | Ei |
Algoritmi ottaa mukaan puuhun ensin kaaret \(2-3\), \(1-2\) ja \(2-4\). Kaari \(1-3\) ei tule mukaan, koska se aiheuttaisi syklin. Sitten mukaan tulee vielä kaari \(4-5\), jonka lisäämisen jälkeen pienin virittävä puu on valmis.
Jos kahdella kaarella on sama paino, Kruskalin algoritmi voi käsitellä ne kummassa tahansa järjestyksessä.
Kruskalin algoritmi voidaan toteuttaa tehokkaasti union-find-rakenteen avulla, koska sen avulla voidaan tarkastaa, tuleeko kaari lisätä mukaan virittävään puuhun. Jos kaaren päissä olevat solmut ovat eri komponenteissa, kaari lisätään virittävään puuhun eikä se aiheuta sykliä.
Seuraava luokka toteuttaa Kruskalin algoritmin:
class Kruskal:
def __init__(self, n):
self.n = n
self.edges = []
def add_edge(self, node_a, node_b, weight):
self.edges.append((node_a, node_b, weight))
def construct(self):
self.edges.sort(key=lambda x: x[2])
uf = UnionFind(self.n)
edges_count = 0
tree_weight = 0
for edge in self.edges:
node_a, node_b, weight = edge
if uf.find(node_a) != uf.find(node_b):
uf.union(node_a, node_b)
edges_count += 1
tree_weight += weight
if edges_count != self.n - 1:
return None
return tree_weight
Metodi construct muodostaa pienimmän virittävän puun ja palauttaa puun painon. Metodi järjestää ensin kaarilistan kaarten painojen mukaan. Tämän jälkeen metodi käy läpi kaaret ja valitsee kaaret puuhun union-find-rakenteen avulla. Kun kaari valitaan puuhun, sen paino lisätään puun painoon.
Virittävä puu on mahdollista muodostaa vain, kun verkko on yhtenäinen. Tämän vuoksi metodi pitää myös kirjaa siitä, montako kaarta on lisätty puuhun. Jos lopussa kaarten määrä on pienempi kuin \(n-1\), verkko ei ole yhtenäinen eikä puuta voinut muodostaa. Tällöin metodi palauttaa arvon None.
Luokkaa voidaan käyttää seuraavasti:
k = Kruskal(5)
k.add_edge(1, 2, 2)
k.add_edge(1, 3, 4)
k.add_edge(2, 3, 1)
k.add_edge(2, 4, 2)
k.add_edge(3, 5, 7)
k.add_edge(4, 5, 5)
print(k.construct()) # 10
Miksi algoritmi toimii?
Kruskalin algoritmi muodostaa virittävän puun ahneesti kaarten painojärjestyksen perusteella. Miksi algoritmi tuottaa varmasti pienimmän virittävän puun?
Tarkastellaan tilannetta, jossa seuraavana järjestyksessä oleva kaari on \(a-b\) ja solmut \(a\) ja \(b\) ovat eri komponenteissa. Jos kaarta \(a-b\) ei valita puuhun, täytyy valita myöhemmin jokin toinen kaari, joka liittää solmut \(a\) ja \(b\) samaan komponenttiin.
Kuitenkin myöhemmin valittu kaari voidaan korvata kaarella \(a-b\) niin, että tuloksena on edelleen virittävä puu. Koska myöhemmin valitun kaaren paino on yhtä suuri tai suurempi kuin kaaren \(a-b\) paino, tämä ei lisää virittävän puun painoa. Niinpä on turvallista valita kaari \(a-b\) puuhun.
Minimointi vs. maksimointi
Verkkojen käsittelyssä minimointi ja maksimointi voivat olla hyvin erilaisia ongelmia. Esimerkiksi lyhin polku kahden verkon solmun välillä voidaan etsiä luvun 14 algoritmeilla, mutta miten voitaisiin löytää pisin polku, joka käy enintään kerran kussakin solmussa?
Mahdollinen tapa etsiä pisin polku olisi muuttaa kaikki kaarten painot negatiivisiksi ja etsiä uudessa verkossa lyhin polku. Tämä ei ole kuitenkaan toimiva tapa, koska uudessa verkossa voisi olla negatiivisia syklejä eivätkä algoritmit pystyisi käsittelemään sitä. Itse asiassa pisimmän polun etsimiseen ei tunneta mitään tehokasta algoritmia.
Virittävien puiden etsimisessä tilanne on kuitenkin toinen, koska suurin virittävä puu (eli virittävä puu, jonka paino on suurin mahdollinen) on helppoa muodostaa muuttamalla kaarten painot negatiivisiksi ja rakentamalla pienin virittävä puu uudessa verkossa. Sama tulos saadaan muuttamalla Kruskalin algoritmia niin, että kaaret käydään läpi käänteisessä painojärjestyksessä.